

Teil 1
Kommen wir nun zu einem nicht ganz einfach aber sehr interessanten Thema - den Rekursionen. Rekursionen gehören eigentlich in das Kapitel der Funktionen. Ich habe es aber erst hier jetzt Verfasst da sie jetzt die Grundlagen von C beherrschen und ich somit mehrere Beispiele zu diesem Kapitel bringen kann.
Kurz gesagt ist eine Rekursion eine Funktion die sich selbst aufruft und sich selbst immer wieder neu definiert. Damit sich aber eine Rekursion nicht ständig selbst aufruft und irgendwann zu einem Ergebnis kommt benötigen wir eine Abbruchbedienung. Sonst kann es irgendwann passieren das Ihr Computer abstürzt da eine Funktion die sich immer wieder selbst Aufruft eine Rücksprungadresse, den Wert der Variable und falls noch nicht freigegeben den Rückgabewert speichert. Und wenn dieser Speicher (Stack) irgendwann mal voll ist geht eben nichts mehr (Stacküberlauf).
Rekursionen sind auch eine Möglichkeit dem Computer zu etwas zu bewegen was Ihn Intelligenter erscheinen lässt. Ein Beispiel ist da z.B. das Schach. Wenn sie einen Zug machen gehen sie doch erst mal alle Möglichkeiten durch die möglich sind um den Gegner möglichst in Bedrängung bzw. den gegnerischen König in Gefahr oder gar Schachmatt zu setzen. Das ist eine logische Denkweise des Menschen. Nun mit Rekursion haben sie ebenfalls die Möglichkeit den Computer eine Situation sooft durchzugehen zu lassen bis er auf eine Lösung kommt, oder auch nicht. Nehmen wir mal an Sie bedrohen den König des Computers. Der Computer geht dann alle Möglichkeiten durch den König aus dieser Bedrohung zu befreien und dann als zweiten Schritt geht er nochmals alle Möglichkeiten durch welche Schritte sie als nächstes theoretisch machen könnten, eben ja nach dem wie tief die Rekursion gehen soll. Jetzt wollen wir mal mit der Praxis beginnen.
Wir wollen eine Funktion schreiben mit der wir 2 Zahlen miteinander teilen. Z.B.: 10/2=5 oder 10/3=3 Rest 1 . Unser Programm darf aber nicht die Operatoren '/' = geteilt und den '%' - Modulo Operator verwenden. Hierzu nun die Rekursive Funktion....
int divide(int x, int y)
{
if(x>=y)
return 1 + divide(x-y,y);
if(x)
printf("Zahl nicht teilbar -> Rest : %d -> ",x);
return 0;
}
Was auf den ersten Blick etwas kompliziert erscheint ist eigentlich halb so wild. Wir wollen das Programm jetzt Schritt für Schritt. Wir gehen jetzt davon aus wir übergeben der Funktion die Werte x=8, und y=2 also rufen wir die Funktion mittels....
printf("8/2 = Ergebnis : %d\n",divide(8,2));
...auf. Als 1. Überprüfen wir das wichtigste in unserer Funktion - die Abbruchbedienung.....
if(x>=y)
Da x=8 und y=2 und die if - Bedienung war ist springen in die nächste Zeile...
return 1 + divide(x-y,y);
Wir geben an unsere Funktion divide den Wert 1 zurück plus den Wert der Funktion divide(x-y,y) . Hoppla werden sie jetzt sagen, richtig erkannt wir rufen hiermit die Funktion divide(int x,int y) erneut auf. Hiermit beginnt die Rekursion. Aber was passiert jetzt eigentlich mit dem Rückgabewert 1? Schauen wir uns das ganze zum besseren Verständnis mal bildlich an...
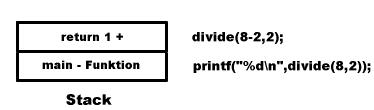
Auf dem Stack wurde zuerst die main - Funktion gelegt, da diese als erstes die Funktion divide aufgerufen hat. Und irgendwo muss ja gespeichert sein wie Ihr Programm wieder zur main - Funktion zurückkommt. Man kann sich das etwa so vorstellen. Bei jedem Funktionsaufruf, egal ob jetzt Rekursiv oder nicht, wird der Aktuelle Zustand der main- Funktion eingefroren und auf dem Stack abgelegt. Damit das Programm aber wieder weis wo die Adresse der main - Funktion wahr wir auf dem Stack immer auch eine Rücksprungadresse mitabgelegt. Ich mache mit der Programmausführung weiter bevor ich sie total verwirre.
Wir haben also unsere Funktion erneut aufgerufen mit...
return 1 + divide(x-y,y);
...also divide(8-2,2) da x=8 und y=2. Jetzt überprüfen wir erneut die Anweisung....
if(x>=y)
Da nun x=6 und y=2 und somit unsere if - Abfrage wieder wahr ist geht die Programmausführung wieder in der nächsten Zeile weiter. Und es geht erneut wieder mit einem Selbstaufruf der Funktion divide() weiter.....
return 1 + divide(x-y,y);
....also wird wieder auf unserem Stack abgelegt....
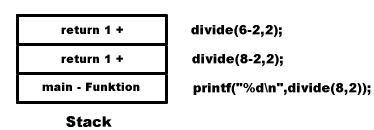
Somit liegen auf unserem Stack 2x der Wert 1 inklusive Rücksprungadresse (die ist hier nicht mitabgebildet). Nun wiederholt sich das ganze Spiel noch zweimal bis es auf unserem Stack folgendermaßen aussieht...

Nun wird erneut die Funktion divide() aufgerufen mit den Werten...
divide(2-2,2)
Jetzt endlich wird unsere Abbruchbedienung...
if(x>=y)
...aktiv. Denn nun ist x=0 und y=2 und somit wir die Programmausführung nicht mehr in der nächsten Zeile ausgeführt. Die nächste Abfrage...
if(x)
...dient nur dazu, falls x ungleich 0 sein sollte, den Rest auszugeben. In unserem Beispiel gibt es keinen Rest. Nun wird an unseren der Wert 0 (return 0) zurückgegeben. Jetzt muss natürlich unser Programm schauen nach dem ein Funktion beendet wurde wo die nächste Rücksprungadresse ist. Schauen wir nochmals unseren Stack an....
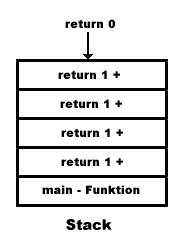
Der Rückgabewert 0 wurde von dem Funktionsaufruf divide(2-2,2) erzeugt. Dorthin führt auch die Rücksprungadresse. Also return 0+1. Die nächste Rücksprungadresse wurde von divide(4-2,2) erzeugt also folgt return 0+1+1. Anschließend folgt return 0+1+1+1 und als letztes return 0+1+1+1+1. Somit könnten wir unseren Stack folgendermaßen aussehen....
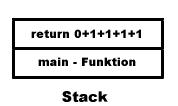
Jetzt bekommt unsere main - Funktion den Rückgabewert 0+1+1+1+1 also 4 und richtig 8/2 ist auch 4.
Toll werden sie jetzt sagen. Und was ist an dem rekursiven Beispiel besser als wenn ich das Programm folgendermaßen schreibe...
/*Download:rek1.c*/ |
Dies Programm erfüllt doch den selben Zweck und ist einfacher. Und sie haben Recht das rekursive Programm ist zum einen schwieriger und zum anderen langsamer, da ständig etwas auf dem Stack gepusht und wieder gepopt werden muss. Und das kann dauern. Mit einem Wort die rekursive Lösung ist die schlechtere Lösung in diesem Beispiel. Schlimmer noch die rekursive Lösung verbraucht viel Speicherplatz zum Anlegen von Parametern, lokale Variablen, Rückgabewerte und Rücksprungadressen. Nehmen wir mal sie wollen die Zahl 1.000.000 durch 2 teilen. Für unsere 2 Parameter x und y benötigen wir schon mal 8 Byte pro Aufruf. Für den Rückgabewert (return 1) benötigen wir 4 Bytes genauso wie für die Rücksprungadresse. Das heißt wir benötigen für eine Ablage auf dem Stack 16 Byte. Nun wenn wir die Zahl 1.000.000 durch 2 teilen bedeutet dies das auf unserem Stack 500.000 Werte ala 16 Bytes liegen. Das sind ca.7,6MB Speicher die wir durch einen Rekursive Aufruf eines solch einfachen Problem verschwenden.
Wozu also Rekursionen anwenden wenn die Iterative Lösung oftmals die bessere ist? In späteren Programmen werden wir einige Beispiele kennen lernen (Binäre Bäume) die eigentlich ohne Rekursion fast gar nicht oder mit unendlich viel Zeilen Code lösbar wären.
Im nächsten Kapitel will ich Ihnen einige einfache rekursive Programme zum besseren Verständnis demonstrieren.


