ein Kapitel zurück                                           ein Kapitel weiter

Backtracking ist ein Verfahren nach dem Trial-and-Error-Verfahren (Versuch und Irrtum) arbeitet. Mit Backtracking versucht man aus Teillösungen systematisch zu einer Komplettlösung zu kommen. Wenn man zum Beispiel aus einer der Teillösung nicht mehr weiterkommt ein Problem zu lösen wird ein oder mehrere Schritte rückgängig gemacht. Die reduzierte Teillösung versucht man dann auf einen anderen Weg wieder aufzubauen. Falls auf diesem Weg wieder eine Sackgasse auftretet gehen wir wieder ein oder mehrer Schritte zurück. So lange bis wir eben zu einer Lösung des Problems kommen oder auch feststellen müssen das es zu diesem Problem keine Lösung gibt. 

#################################################
#C *                                            #
#  *                    *                       #
#                                               #
#     *        *   *                        *   #
#            *         *                        #
# *        *   *                 *              #
#                                               #
#   *   *    *       *             *            #
# *                                             #
#           * *                      *          #
#                  *                      *  *  #
#        *       *        *                    o#
#################################################

Wir wollen hier das 'C' (Pacman)zum Zeichen 'o' (Essen) bringen. Die '*'-Zeichen sollen Hindernisse für unseren Pacman darstellen. Das ganze Spielfeld wollen wir auf einem zweidimensionalen char - Array darstellen... 

char spielfeld[15][50];

...also 15 Zeilen und 50 Spalten. Wir wollen unseren Pacman vorerst in 4 Richtungen bewegen lassen können....




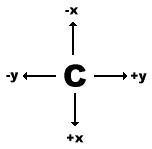
Also benötigen wir 4 Funktionsselbstaufrufe. Für jede Richtung eine. Eine für Richtung x+ (1 Zeile runter), x- (1 Zeile hoch), y+ (Eine Spalte nach Rechts), y- (Eine Spalte nach Links). Die 4 Funktionsselbstaufrufe sehen deshalb in etwa so aus.... 

step(x,y+1);
step(x+1,y);
step(x-1,y);
step(x,y-1);

Damit hätten wir für jede Richtung einen Funktionsselbstaufruf. Jetzt übergeben wir noch, nur für die Grafische Darstellung, an die Funktion die alten Positionen von x und y.... 

step(x,y+1,xalt=x,yalt=y);
step(x+1,y,xalt=x,yalt=y);
step(x-1,yxalt=x,yalt=y,);
step(x,y-1,xalt=x,yalt=y,);

xalt und yalt dienen nur der Grafischen Darstellung. Mit Backtracking hat das aber jetzt nichts zu tun. Nun müssen wir festlegen in welche Richtung und wohin unser Pacman als erstes gehen soll. Da unser Pacman an der Position [1][1] ist und unser Essen an der Position [13][48] können wir uns überlegen ob wir als erstes in Richtung y+1 (1 Spalte nach rechts) oder x+1 (1 Zeile nach unten) gehen. Ich habe mich zuerst für die Richtung y+1 (1 Spalte nach rechts) entschieden. Bevor wir aber zuerst in die Richtung y+1 gehen müssen wir überprüfen ob in dieser Richtung ein Hindernis (*) ist oder ob wir das Ende des Spielfeldes bereits erreicht haben. Zusätzlich müssen wir noch überprüfen ob unsere alte Spalte (yalt) nicht schon einen Funktionsaufruf zuvor besucht wurde (yalt!=y+1) . Zusätzlich wird, wenn alle Bedienungen erfüllt sind die Funktion erneut aufgerufen 'step(x,y+1,x,y)'. Entscheidend ist nun ob der erneute Funktionsaufruf als Rückgabewert 1 (return 1) oder 0 (return 0) liefert. Wird 1 zurückgegeben wird der Zug ausgeführt. Aber das bringt Ihnen jetzt gar nichts bevor sie die fertige Funktion nicht kennen. Hier jetzt der 1. Funktionsaufruf..... 

if(y+1<49 && spielfeld[x][y+1] !='*' && yalt!=y+1 && step(x,y+1,x,y))
    return 1;

Die nächsten drei if-else-Anweisung sehen ähnlich aus mit dem einzigen Unterschied das jede für eine andere Richtung bestimmt ist. Hier nun die die nächsten 3 Anweisungen für die Richtung 'x+,x- und y-' .... 

else if(x+1<14 && spielfeld[x+1][y] !='*' && xalt!=x+1 && step(x+1,y,x,y))
               return 1;
else if(x-1>0 && spielfeld[x-1][y] !='*' && xalt!=x-1 && step(x-1,y,x,y))
               return 1;
else if(y-1>0 && spielfeld[x][y-1] !='*' && yalt!=y-1 && step(x,y-1,x,y))
               return 1;

Falls keine dieser 4 Aufrufe Erfolgreich war wird an die vorangegangene Funktion der Wert 0 (return 0) zurückgegeben und das heißt das dieser vorangegangen Funktionsaufruf (Zug) nicht ausgeführt wird. Die Abbruchbedienung haben wir wenn unser Pacman 'C' auf der selben Position ist wie 'o' auf dem Spielfeld. "Abgebrochen" wird aber auch wenn das Labyrinth zu komplex ist und unser Pacman Paartour nicht ans Ziel finden will oder er in einer Sackgasse festhängt wo es kein zurück mehr gibt. Leider bedeutet dieser Abbruch einen Stacküberlauf. Hier die komplette Funktion..... 

int step(int x,int y,int xalt,int yalt)
{

 /*kann bei Unix durch usleep und bei MSDOS durch delay ersetzt werden*/
 printf("<ENTER>");  getchar();
 if(spielfeld[x][y]=='O') /*sind wir am Ziel?*/
  {

   spielfeld[x][y]='C';
   spielfeld[xalt][yalt]=' ';
   showspielfeld();
   printf("Pacman zuhause!\n");
   exit (1);
  }
 else if(spielfeld[x][y]==' ')
  {

   spielfeld[x][y]='C';
   spielfeld[xalt][yalt]=' ';
   showspielfeld();

   if(y+1<49 && spielfeld[x][y+1] !='*' && yalt!=y+1 && step(x,y+1,x,y))
        return 1;
   else if(x+1<14 && spielfeld[x+1][y] !='*' && xalt!=x+1 && step(x+1,y,x,y))
        return 1;
   else if(x-1>0 && spielfeld[x-1][y] !='*' && xalt!=x-1 && step(x-1,y,x,y))
        return 1;
   else if(y-1>0 && spielfeld[x][y-1] !='*' && yalt!=y-1 && step(x,y-1,x,y))
        return 1;
  }
 return 0;
}

Wollen wir zum Test kurz ein paar Durchläufe machen. Zuerst übergeben wir an die Funktion... 

step(1,1,1,1);

Somit gäbe sich in etwa folgendes Beispiel.... 

#############
#C  *
#        *      *
#  *       *       *
#*    *         *



Pacman ist an Position 1,1

Als erstes wird überprüft ob wir am Ziel sind.... 

if(spielfeld[x][y]=='O')

danach wird überprüft ob die Position [x][y] frei sind... 

else if(spielfeld[x][y]==' ')

Wenn ja wir unser Pacman 'C' dort hingesetzt und es sieht aus wie in der linken Abbildung oben. Jetzt wird überprüft in welche Richtung Pacman gehen kann.... 

if(y+1<49 && spielfeld[x][y+1] !='*' && yalt!=y+1 && step(x,y+1,x,y))

Ja die Richtung y+1 ist frei und wurde auch nicht zuvor besucht. Somit liegt auf dem Stack jetzt folgendes.... 

step(1,1+1,1,1)

Dieser Wert wartet jetzt um Ausgeführt zu werden auf den Rückgabewert 1. Schon geht es zum nächsten Funktionsaufruf. Folgende Schritte haben wir bisher gemacht (von unten nach oben).... 

step(1,3+1,1,1)
step(1,2+1,1,1)
step(1,1+1,1,1)

Nun sieht das bildlich folgendermaßen aus.... 

#############
#  C*
#        *      *
#  *       *       *
#*    *         *

Nun kann man erkennen das Pacman ein Hindernis ('*') vor sich hat. Also wir die erste if - Anweisung dieses mal nicht zum Zuge kommen. Wie sieht es mit der 2. aus? 

else if(x+1<14 && spielfeld[x+1][y] !='*' && xalt!=x+1 && step(x+1,y,x,y))

Können wir eine Zeile tiefer gehen (x+1)? Ja wir können somit wird nun... 

step(x+1,y,x,y)

...aufgerufen. Somit sieht's mit Pacman folgendermaßen aus..... 

#############
#   *
# C      *      *
#  *       *       *
#*    *         *

Somit wäre Pacman momentan an Position [2][3]. Sie können das ganze ja mal ein paar Schritte Weiterdurchgehen. Ich habe Ihnen dazu jetzt auch ein Programm geschrieben womit sie das ganze Beispiel am Bildschirm demonstriert bekommen.... 

/*Download:baktrak.c*/

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#ifdef __MSDOS__
  #include <conio.h>
#else
  #define clrscr() printf("\x1B[2J")
#define HINDERNISSE 100

char spielfeld[15][50];

void createspielfeld(void)
{

 int i,j,x,y;
 for(i=0,j=0;j<50;j++)
   spielfeld[i][j]='#';

 for(i=1;i<15;i++)
   for(j=0;j<50;j++)
    {

     if(j==0 || j==49)
       spielfeld[i][j]='#';
     else
       spielfeld[i][j]=' ';
     if(i==13 && j==48)
       spielfeld[i][j]='O';
     }
 for(i=14,j=0;j<50;j++)
   spielfeld[i][j]='#';

 for(i=0;i<=HINDERNISSE;i++)
  {

   x=rand()%14;
   y=rand()%48;
   if(x<15&&y<50 && x>0&&y>0)
      spielfeld[x][y]='*';
   }
 spielfeld[1][1]=' ';
}

void showspielfeld(void)
{

 int i,j;
 clrscr();
 for(i=0;i<15;i++)
  for(j=0;j<50;j++)
   {

    printf("%c",spielfeld[i][j]);
    if(j==49)
      printf("\n");
   }
}

int step(int x,int y,int xalt,int yalt)
{

 printf("<ENTER>");
 getchar();

 if(spielfeld[x][y]=='O') /*sind wir am Ziel?*/
  {

   spielfeld[x][y]='C';
   spielfeld[xalt][yalt]=' ';
   showspielfeld();
   printf("Pacman zuhause!\n");
   exit (1);
  }
 else if(spielfeld[x][y]==' ')
  {

   spielfeld[x][y]='C';
   spielfeld[xalt][yalt]=' ';
   showspielfeld();

   if(y+1<49 && spielfeld[x][y+1] !='*' && yalt!=y+1 && step(x,y+1,x,y))
         return 1;
   else if(x+1<14 && spielfeld[x+1][y] !='*' && xalt!=x+1 && step(x+1,y,x,y))
         return 1;
   else if(x-1>0 && spielfeld[x-1][y] !='*' && xalt!=x-1 && step(x-1,y,x,y))
         return 1;
   else if(y-1>0 && spielfeld[x][y-1] !='*' && yalt!=y-1 && step(x,y-1,x,y))
         return 1;
  }  spielfeld[x][y]=' ';
 return 0;
}

int main()
{

 createspielfeld();
 step(1,1,1,1);

 return 0;
}

Nun der Code ist stark auf einem Rechtdrang ausgerichtet, wenn sie Pacman in eine andere Richtung schicken wollen müssen sie das Backtracking Ihren Bedürfnissen anpassen. Erhöhen sie mal die Anzahl der HINDERNISSE und sie werden merken das unser Pacman irgendwann auch keinen Ausweg mehr findet obwohl es eigentlich einen gäbe. Das heißt Pacman dreht sich im Kreis. Nun haben wir als eine Möglichkeit den Code noch mehr zu verkomplizieren oder wir machen Pacman noch eine Spur "Intelligenter" und lassen in auch noch in allen Richtungen diagonal laufen. Somit kann sich Pacman in 8 Richtungen fortbewegen....




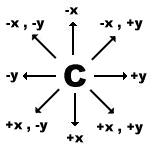
Somit hätten wir folgende 4 neue Koordinaten.... 

rechtshoch(x-1,y+1)
rechtsrunter(x+1,y+1)
linksrunter(x+1,y-1)
linkshoch(x-1,y-1)

Jetzt müssen wir erneut die Reihenfolge zusammensetzten damit wir auf den schnellsten Weg ins Ziel kommen. Unser Ziel ist rechts unten somit sollten wir diese Richtung als Priorität benutzen. Ich schlage folgenden Weg vor.... 

if(rechts=frei)
else if(rechtsrunter=frei)
else if(rechtsoben=frei)
else if(nachunten=frei)
else if(linksrunter=frei)
else if(oben=frei)
else if(links=frei)
else if(linksoben=frei)
else return 0

Wenn jemand einen besseren Vorschlag dazu hat würde mich freuen. Nun wollen wir das ganze in unsere Funktion einbauen.....

int step(int x,int y,int xalt,int yalt)
{

 printf("<ENTER>");
  getchar();

 if(spielfeld[x][y]=='O') /*sind wir am Ziel?*/
  {

   spielfeld[x][y]='C';
   spielfeld[xalt][yalt]=' ';
   showspielfeld();
   printf("Pacman zuhause!\n");
   exit (1);
  }
 else if(spielfeld[x][y]==' ')
  {

   spielfeld[x][y]='C';
   spielfeld[xalt][yalt]=' ';
   showspielfeld();
   if(y+1<49 && spielfeld[x][y+1] !='*'
       && yalt!=y+1 && step(x,y+1,x,y))   /*rechts*/
     return 1;
   else if(y+1<49&&x+1<14 && spielfeld[x+1][y+1] !='*'
           && xalt!=x+1 && yalt!=y+1 && step(x+1,y+1,x,y))
     return 1;/*rechtsrunter*/
   else if(x-1>0&&y+1<49&&spielfeld[x-1][y+1]!='*'
           &&xalt!=x-1&&yalt!=y+1&&step(x-1,y+1,x,y))
      return 1;/*rechtsoben*/
   else if(x+1<14 && spielfeld[x+1][y] !='*'
           && xalt!=x+1 && step(x+1,y,x,y))
      return 1;/*nach unten*/
   else if(x+1<14&&y-1>0&&spielfeld[x+1][y-1]!='*'
           &&xalt!=x+1&&yalt!=y-1&&step(x+1,y-1,x,y))
      return 1;/*linksrunter*/
   else if(x-1>0 && spielfeld[x-1][y] !='*'
           && xalt!=x-1 && step(x-1,y,x,y))
      return 1;/*nach oben*/
   else if(y-1>0 && spielfeld[x][y-1] !='*'
           && yalt!=y-1 && step(x,y-1,x,y))
      return 1;/*nach links*/
   else if(x-1>0&&y-1>0&&spielfeld[x-1][y-1] !='*'
           &&xalt!=x-1&&yalt!=y-1&&step(x-1,y-1,x,y))
      return 1;/*linksoben*/
  }
  spielfeld[x][y]=' ';
 return 0;
}

Mit 8 Wegen schafft unser Pacman nun schon mehrere Hindernisse auf einmal. Aber ab einer gewissen Anzahl von Hindernisse happerts auch hier wieder obwohl wir noch nicht in eine Sackgasse gekommen sind. Also benötigen wir noch eine Funktion die sich merkt ob wir ein Feld bereits besucht haben oder nicht. Dies stellt sich als einfaches Unterfangen da. Wir benutzen ein weiteres zweidimensionales Array..... 

int besucht[15][50];

Alle Felder initialisieren wir mit dem Wert 0. Jetzt müssen wir nur noch in unserem Programm nur noch die Position die wir bereits besucht haben den Wert 1 übergeben. Jetzt können wir in unseren if-else-Anweisungen noch die Abrage einbauen... 

...&& besucht != 1 &&....

Sie können das Verbesserte Programm hier herunterladen ....


Dowbload : baktrak2.c
baktrak2.c


Danke muss ich auch an Wolfgang von www.pro-linux.de sagen der mir mit 2-3 Sätzen das Prinzip von Backtracking erklärt hat....

Du musst einen Wert (z.B. "1") zurückgeben, wenn du am Ziel bist und den gleichen, wenn der Weg, den du probiert hast zum Ziel führte. Wenn du in einer Sackgasse bist, musst du einen logisch anderen Wert zurückgeben (in dem Fall also "0"). Einen Weg, den du mal gegangen bist, darfst du nun nicht zurückgehen (da er bekanntlich nicht zum Ziel führt. Mit dieser Strategie kommst du in einem beliebig komplexen Irrgarten immer zum Ziel (sofern ein Weg zum Ziel existiert und der Irrgarten nicht so komplex ist, Das es einen Stack-Überlauf gibt ;-)).

Wem das jetzt zu kompliziert war für dem habe ich noch einen 2.Teil im nächsten Kapitel zu Backtracking geschrieben. Das "8 Dame Problem".

ein Kapitel zurück          nach oben           ein Kapitel weiter


© 2001,2002 Jürgen Wolf