24.3 Sortieralgorithmen 

Viele Programme und Computer (Server) erledigen oft den lieben langen Tag nichts anderes, als Daten zu sortieren. Wenn das Sortieren verstanden ist, wird es nicht mehr schwer fallen, andere Algorithmen zu verstehen. Sortieren könnte man sozusagen auch als Basic für Algorithmen bezeichnen. Hier einige Typen von Sortieralgorithmen:

Internes Sortieren – internes Sortieren findet innerhalb des RAMs (Arbeitsspeicher) statt. Dabei werden meist Daten an das Programm geschickt und werden sortiert wieder ausgegeben.

Externes Sortieren – beim externen Sortieren werden externe Speicherquellen (Festplatte, Streamer, Tape, ...) verwendet. Während des externen Sortierens werden zahlreiche Lese- und Schreibzugriffe auf externe Quellen ausgeführt. Externes Sortieren wird genutzt, wenn die Daten zum Sortieren nicht auf einmal im RAM verarbeitet werden können.

Vergleichendes Sortieren – dabei wird häufig ein Schlüssel zum Sortieren verwendet. Dieser Schlüssel besteht meist nur aus einem kleinen Teil der Daten, der das Sortieren steuert.

Stabiles Sortieren – stabil wird sortiert, wenn z.B. eine Arbeitnehmerliste, die nach Alphabet sortiert ist, nach Gehalt sortiert wird, ohne dass dabei die alphabetische Liste durcheinander gerät.

Im Folgenden werden häufig Arrays zum Sortieren verwendet. Diese sollten Sie sich als Schlüssel einer Datenstruktur vorstellen. Die Funktionen sind so aufgebaut, dass sie jederzeit mit ein wenig Tipparbeit an die eigenen Bedürfnisse angepasst werden können. Primär geht es darum, Ihnen die einzelnen Sortierverfahren näher zu bringen, speziell deren Funktionen. Die Implementierung ist zumeist problemabhängig und richtet sich nach der Art der Daten, die es zu sortieren gilt.

24.3.1 Selektion Sort – Sortieren durch Auswählen 

Der erste Sortieralgorithmus ist »Selektion Sort«. Dieser Algorithmus sucht sich als Erstes das kleinste Element in der Liste, merkt es sich und tauscht es gegen das Element am Anfang aus, sodass sich dann das kleinste Element ganz am Anfang befindet. Als Nächstes wird das zweitkleinste Element in der Liste gesucht und wird gegen das an zweiter Stelle platzierte Element der Liste ausgetauscht usw.

Auf diese Weise haben immer die Elemente auf der linken Seite der aktuellen Position einen festen Platz und werden nicht mehr geändert. Hier der Vorgang bildlich:

Hier klicken, um das Bild zu Vergrößern

Abbildung 24.1   Sortieren durch Auswählen

Es folgt jetzt der Quellcode:

/* selektion.c */
#include <stdio.h>
#include <stdlib.h>
void selection(int *array, int elemente) {
   int index,index_klein,
       wert, wert_klein;
   /* Schleife durchläuft von links nach rechts */
   for(index = 0; index < elemente; index++) {
      /* Aktuelle Position */
      wert=index;
      /* Schleife durchläuft bis kleineres Element als
       * aktuelle Pos. gefunden wurde oder bis zum Ende,
       * was bedeutet, die aktuelle Position ist schon
       * das kleinste */
      for(index_klein = index+1; index_klein <= elemente;
        index_klein++) { /* Ein kleineres Element gefunden? */
         if(array[index_klein] < array[wert])
            /* Neues kleinstes Element */
            wert=index_klein;
      }
      /* Kleinstes Element an die aktuelle
       * Position falls nötig */
      if(wert != index) {
         wert_klein=array[wert];
         array[wert]=array[index];
         array[index]=wert_klein;
      }
   }
}
int main(void) {
   int i;
   /* Das Array zum Sortieren */
   int test_array[] = { 5, 2, 7, 9, 1, 4, 3, 8, 6 };
   int N = sizeof(test_array)/sizeof(int);
   selection(test_array, N-1);
   for(i = 0; i < N; i++)
      printf("%d ", test_array[i]);
   printf("\n");
   return EXIT_SUCCESS;
}

Natürlich können Sie mit »Selektion Sort« auch andersherum sortieren, also vom größten Element abwärts. In diesem Fall muss nur die if-Abfrage geändert werden:

if(array[index_klein] > array[wert])

Der Vorteil von »Selektion Sort« liegt darin, dass jedes Element höchstens einmal bewegt wird.

24.3.2 Insertion Sort 

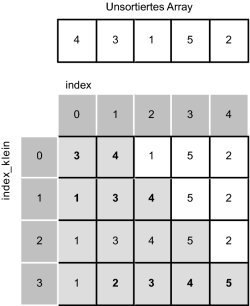
Das Prinzip von »Insertion Sort« (=sortieren durch direktes Einfügen) ist relativ einfach. Die einzelnen Elemente werden wieder von vorne nach hinten durchlaufen. Von der aktuellen Position aus wird jedes Element von rechts nach links weitergereicht. Und das so lange, bis das bewegte Element größer oder gleich dem Element ist, das an der im Augenblick abgefragten Position liegt.

Der Platz für das Element, das verschoben wird, ist frei. Diese Lücke wird mit dem entsprechenden Wert an der richtigen Stelle gefüllt. Bildlich können Sie sich »Insertion Sort« folgendermaßen vorstellen:

Hier klicken, um das Bild zu Vergrößern

Abbildung 24.2   Insertion Sort

Der folgende Quellcode soll diesen Algorithmus noch verständlicher machen:

/* insertion.c */
#include <stdio.h>
#include <stdlib.h>
void insertion(int *array, int elemente) {
   int index,index_klein,wert_klein;
   /* Schleife von links-1 nach rechts */
   for(index=1; index<=elemente; index++) {
      /* aktuelle Position zwischenspeichern */
      wert_klein=array[index];
      /* Kleineren Wert als wert_klein suchen. Schleife
       * durchläuft von aktueller Pos. von rechts nach links */
      for( index_klein=index;
           array[index_klein-1] > wert_klein&&index_klein > 0;
           index_klein-- )
         /* Wenn Vorgänger größer als aktuelles
          * Element in wert_klein */
         array[index_klein] = array[index_klein-1];
      /* gespeichertes Element an neue Position ->
       * Lücke auffüllen */
      array[index_klein]=wert_klein;
   }
}
int main(void) {
   int i;
   /* Das Array zum Sortieren */
   int test_array[] = { 5, 2, 7, 9, 1, 4, 3, 8, 6 };
   int N = sizeof(test_array)/sizeof(int);
   insertion(test_array, N-1);
   for(i = 0; i < N; i++)
      printf("%d ", test_array[i]);
   printf("\n");
   return EXIT_SUCCESS;
}

Hier klicken, um das Bild zu Vergrößern

Abbildung 24.3   Geklammerte Werte symbolisieren den Elementetausch

Das aktuelle Element wird hier in wert_klein gespeichert. Jetzt wird so lange umdisponiert, bis entweder ein Element kleiner als wert_klein ist, oder bis Sie am Anfang des Arrays (Index 0) angekommen sind (was bedeuten würde wert_klein ist das kleinste Element im Array).

Wie auch schon bei »Selektion Sort« sind die Elemente bei »Insertion Sort« auf der linken Seite sortiert; nur mit dem Unterschied, dass dies noch keine endgültige Stellung wie bei »Selektion Sort« bedeutet.

24.3.3 Bubble Sort 

»Bubble Sort« ist ein recht einfaches Sortierverfahren. Dabei wird das vollständige Array durchlaufen, und jedes Mal – wenn notwendig – werden die benachbarten Elemente miteinander getauscht.

Nach jedem Durchlauf bekommt immer das letzte Element einen festen Platz. Daher macht es auch Sinn, eine rückwärts zählende Schleife von dieser Position an einzusetzen. Hier der Quellcode zu »Bubble Sort«:

/* bubble.c */
#include <stdio.h>
#include <stdlib.h>
void bubble(int *array, int elemente) {
   int i,temp;
   while(elemente--)
      for(i = 1; i <= elemente; i++)
         if(array[i-1] > array[i]) {
            temp=array[i];
            array[i]=array[i-1];
            array[i-1]=temp;
         }
}
int main(void) {
   int i;
   /* Das Array zum Sortieren */
   int test_array[] = { 5, 2, 7, 9, 1, 4, 3, 8, 6 };
   int N = sizeof(test_array)/sizeof(int);
   bubble(test_array, N);
   for(i = 0; i < N; i++)
      printf("%d ", test_array[i]);
   printf("\n");
   return EXIT_SUCCESS;
}

Da nach jedem Durchlauf das größte Element ganz nach rechts geholt wird und dies nicht mehrmals verglichen werden sollte, wurde von dieser Position aus eine rückwärts zählende Schleife eingesetzt:

while(elemente--)

Hier die grafische Darstellung von »Bubble Sort«:

Hier klicken, um das Bild zu Vergrößern

Abbildung 24.4   Bubble Sort in Aktion

Auf die letzten Durchläufe wurde in der Darstellung verzichtet, da keine Daten mehr verschoben werden.

24.3.4 Shellsort 

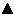
»Shellsort« ist eine Erweiterung von »Insertion Sort«. Anstatt jedes benachbarte Element wie bei »Insertion Sort« zu vergleichen und zu sortieren, vergleicht »Shellsort« jedes n-te Element (bei beliebigem Anfangselement). Damit ist es möglich, Elemente zu sortieren, die in größeren Entfernungen voneinander liegen. Ist der Abstand für n beispielsweise 4, dann setzen sich folgende Gruppen von Elementen mit dem Index 0, 4, 8, 12 … und 1, 5, 9, 13 … 2, 6, 10, 14 … 3, 7, 11, 15 … usw. zusammen. Diese Gruppen werden einzeln sortiert. Danach wird n verringert, und dann werden die Gruppen n-1 sortiert. So lange, bis n==1 ist, und somit im letzten Durchlauf keine Unterteilung mehr stattfindet. Ist n gleich von Anfang an 1, könnten Sie sich den Aufwand sparen, da dies dem »Insertion Sort«-Algorithmus entspräche.

Natürlich ist n abhängig von den Werten, die sortiert werden. Man spricht dabei von Distanzfolgen. Je besser diese Folge, desto schneller werden die Daten sortiert. Die Suche nach der optimalen Folge ist Aufgabe des Programmierers. Hier der Quellcode zu »Shellsort«:

/* shellsort.c */
#include <stdio.h>
#include <stdlib.h>
void shellsort (int *array, int elemente) {
  int i, j, temp, n;
   /* Anfangswert für die Distanz errechnen */
  for ( n = 1; n <= elemente/9; n = 3*n+1);
  for (; n > 0; n /= 3) {
     for (i = n; i <= elemente; i++) {
        temp = array[i];
        /* Größer als temp und nicht elemente
         * sowie >= und nicht > */
        for(j = i;
            j >= n && array[j-n] > temp;
            j -= n) {
           array[j] = array[j-n];
        }
        array[j] = temp;
     }
  }
}
int main(void) {
   int i;
   /* Das Array zum Sortieren */
   int test_array[] = { 5, 0, 2, 7, 9, 1, 4, 3, 8, 6 };
   int N = sizeof(test_array)/sizeof(int);
   shellsort(test_array, N-1);
   for(i = 0; i < N; i++)
      printf("%d ", test_array[i]);
   printf("\n");
   return EXIT_SUCCESS;
}

Jetzt soll gezeigt werden, wie Sie die optimale Distanzfolge von Daten für »Shellsort« ermitteln. Es wird ein Array mit 10 Millionen Elementen erstellt, welches Zahlen in absteigender Reihenfolge enthält. In diesem Fall müssten alle Elemente bei der Sortierung ausgetauscht werden. Getestet wird mithilfe einer Schleife und den Distanzfolgen von 2 bis 10.

Für das Profiling wird hierbei die Funktion clock() verwendet, welche für diesen Zweck vollkommen ausreichen dürfte (mehr zum Profiling entnehmen Sie bitte dem entsprechenden Abschnitt 21.2, Laufzeitmessung (Profiling).

Hier das Beispiel mit den verschiedenen Distanzfolgen:

/* profile_shellsort.c */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10000000
#define MAX_TEST 10
/* Das Array zum Sortieren */
int test_array[MAX];
void init_test_array(void) {
   int i,j;
   for(i = MAX, j = 0; i >= 0; i--,j++)
      test_array[j] = i;
}
void shellsort(int *array, int elemente, int distanz) {
   int i, j, temp, n = elemente;
   for(; n > 0; n /= distanz)
      for (i = n; i <= elemente; i++) {
         temp = array[i];
         /* Größer als temp und nicht elemente
          * sowie >= und nicht > */
         for(j = i;
             j >= n && array[j-n] > temp;
             j -= n) {
            array[j] = array[j-n];
         }
         array[j] = temp;
      }
}
int main(void) {
   int distanz_folge;
   float zeit;
   clock_t start, ende;
   for(distanz_folge =2;
     distanz_folge <= MAX_TEST; distanz_folge++) {
      init_test_array();
      start = clock();
      shellsort(test_array, MAX-1, distanz_folge);
      ende = clock();
      /* Ergebnis der Laufzeitmessung in Sekunden */
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Die Laufzeitmessung der Distanzfolge "
         " %d ergab %2.2f  Sekunden\n" ,distanz_folge,zeit);
   }
   return EXIT_SUCCESS;
}

Je nach Power des Rechners erhalten Sie folgende Ausgabe (als Beispiel ein 1700 MHz Pentium 4, 256 MB RAM):

Hier klicken, um das Bild zu Vergrößern

Abbildung 24.5   Ermitteln der optimalen Distanzfolge von Shellsort

In diesem Fall scheint eine Distanzfolge zwischen 3 und 6 das optimalste Ergebnis zu liefern.

Diese Tests der Laufzeitmessungen mit Shellsort werden Sie wohl immer durchführen müssen, da bisher noch niemand in der Lage war, Shellsort genau zu analysieren. Aber verglichen mit Insertion Sort läuft Shellsort immer schneller ab. Zum Vergleich kann hierbei Insertion Sort (Distanzfolge = 1) mit eingebaut werden. Dabei sollte aber die Anzahl der Elemente reduziert werden, weil Insertion Sort eine Weile mit ihnen beschäftigt sein wird.

24.3.5 Quicksort 

Ein oft eingesetzter Algorithmus ist Quicksort, da seine Implementierung nicht allzu schwer ist. Aufgrund ihrer häufigen Verwendung wurde diese Funktion in die ANSI C-Bibliothek mit aufgenommen (qsort). Quicksort funktioniert nach dem Prinzip »Teile und herrsche«, also rekursiv. Die Daten werden immer in zwei Teile zerlegt und wieder sortiert. Diese zwei Teile werden wiederum jeweils in zwei Teile zerlegt und sortiert usw., bis die Daten sortiert sind. Die Rekursion beendet sich, wenn das Teilstück aus nur noch einem Element besteht. Hierzu der Quellcode von Quicksort:

/* quicksort.c */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 50000
/* Das Array zum Sortieren */
int test_array[MAX];
void my_qsort(int*, int*);
void init_test_array(void) {
   int i, j;
   for(i = MAX,j=0; i >= 0; i--,j++)
      test_array[j] = i;
}
void print_test_array(void) {
   int i;
   for(i=0;i<MAX; i++)
      printf("%d ",test_array[i]);
}
/* Die Funktion erhält einen Zeiger auf das erste
 * und eine zweiten Zeiger auf das letzte Element.
 * Hier werden dazu die Namen links und rechts verwendet
 */
void my_qsort(int *links, int *rechts) {
   int *ptr1 = links;
   int *ptr2 = rechts;
   int w, x;
   /* x bekommt die Anfangsadresse der
    * Mitte von links und rechts
    * Anstatt der Bitverschiebung hätten Sie
    * auch einfach geteilt durch 2 rechnen können.
    */
   x = *(links + (rechts – links >> 1));
   do {
      while(*ptr1 < x) ptr1++;
      while(*ptr2 > x) ptr2--;
      if(ptr1 > ptr2)
         break;
      w = *ptr1;
      *ptr1 = *ptr2;
      *ptr2 = w;
   } while(++ptr1 <= --ptr2);
   if(links < ptr2)  my_qsort(links, ptr2);
   if(ptr1 < rechts) my_qsort(ptr1, rechts);
}
int main(void) {
   init_test_array();
   my_qsort(test_array, test_array+MAX);
   print_test_array();
   return EXIT_SUCCESS;
}

Im Gegensatz zu den anderen bisher verwendeten Algorithmen sieht dieser schon ein wenig kryptischer aus. Daher soll er auch etwas genauer analysiert werden. Es wird von folgenden unsortierten Werten ausgegangen:

Hier klicken, um das Bild zu Vergrößern

Abbildung 24.6   Werte sollen mit Quicksort sortiert werden

Aufgerufen wird die Funktion mit:

my_qsort(test_array, test_array+MAX);

Somit zeigt in der Funktion my_qsort() der Zeiger links auf die Anfangsadresse von test_array, nämlich den Wert 20. Der rechte Zeiger verweist auf das Ende des Arrays, also den Wert 320. In der Funktion übernehmen zwei Zeiger diese Adressen:

int *ptr1 = links;
int *ptr2 = rechts;

Durch die darauf folgende Berechnung

x = *(links + (rechts – links >> 1));

bekommt die Variable x zunächst den Wert 100 zugewiesen. Denn im Klartext ergibt diese Rechnung auf Zahlen bezogen:

x = *(0 + (7 – 0 / 2));

Das Ergebnis dieser Berechnung beträgt 3, und die Zahl mit dem Index [3] lautet 100. Weiter geht es mit folgender Zeile:

while(*ptr1 < x) ptr1++;

Der Zeiger ptr1 wird jetzt so lange inkrementiert, bis er auf ein Element zeigt, das größer als oder gleich dem Element von x ist. Im aktuellen Beispiel ist dies der Wert 400.

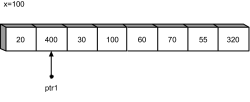
Hier klicken, um das Bild zu Vergrößern

Abbildung 24.7   ptr1 ist auf einen Wert gestoßen, der größer als x ist

Genauso verläuft dies mit dem Zeiger ptr2:

while(*ptr2 > x) ptr2--;

Dieser wird so lange dekrementiert, bis er auf ein Element zeigt, welches kleiner als oder gleich dem von x ist.

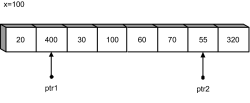
Hier klicken, um das Bild zu Vergrößern

Abbildung 24.8   ptr2 ist auf einen Wert gestoßen, der kleiner als x ist

Als Nächstes wird überprüft, ob ptr1 schon weiter ist als ptr2. Trifft dies zu, wird die do-while-Schleife abgebrochen. Hier stimmt dies aber nicht, und somit werden die beiden Elemente, auf die ptr1 und ptr2 zeigen, vertauscht:

w = *ptr1;
*ptr1 = *ptr2;
*ptr2 = w;

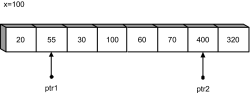
Hier klicken, um das Bild zu Vergrößern

Abbildung 24.9   Werte von ptr1 und ptr2 tauschen

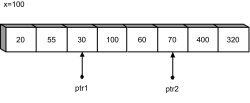
Jetzt bewegen sich die beiden Zeiger aufeinander zu mit

++ptr1 <= --ptr2

Hier klicken, um das Bild zu Vergrößern

Abbildung 24.10   Die Zeiger nähern sich einander

Danach folgen wieder

while(*ptr1 < x) ptr1++;
while(*ptr2 > x) ptr2--;

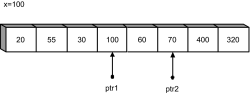
Die Bedingung für den Zeiger ptr1 trifft bereits nach der ersten Inkrementierung zu (100<60), und der zweite Zeiger wird gar nicht dekrementiert (70>100). So ergibt sich folgender Zustand:

Hier klicken, um das Bild zu Vergrößern

Abbildung 24.11   Wieder sind zwei Werte ausgemacht, wo ptr1 nicht kleiner und ptr2 nicht größer als x sind

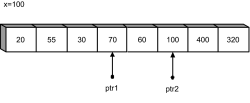
Jetzt werden wieder beide Elemente ausgetauscht:

Hier klicken, um das Bild zu Vergrößern

Abbildung 24.12   ptr1 und ptr2 nach dem Wertetausch

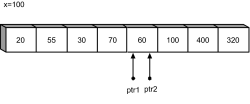
Danach werden beide Zeiger wieder aufeinander zu bewegt, sodass sich jetzt folgendes Bild ergibt:

Hier klicken, um das Bild zu Vergrößern

Abbildung 24.13   ptr1 und ptr2 treffen aufeinander

Nach den beiden Zeilen

while(*ptr1 < x) ptr1++;
while(*ptr2 > x) ptr2--;

ist jetzt die if-Bedingung (ptr1 > ptr2) wahr und bricht mit break die do-while-Schleife ab. Folgender Zustand liegt dabei vor:

Hier klicken, um das Bild zu Vergrößern

Abbildung 24.14   Ein Teilungsprozess findet statt

Damit wurde der erste Teilungsprozess beendet. Daran lässt sich auch schon feststellen, dass alles, was sich links von der Teilungslinie befindet, größer, und alles, was rechts davon liegt, kleiner ist. Der Algorithmus funktioniert auch, wenn der Wert der Variablen x bspw. einem Wert entspricht, der weiter außen liegt. Die optimalste Bedingung ist eine Teilung in der Mitte.

Hier klicken, um das Bild zu Vergrößern

Abbildung 24.15   Quicksort ist abhängig von der Anordnung der Daten

Nach der ersten Teilung sind nun weitere Schritte notwendig. Oder einfacher ausgedrückt: Im Prinzip sind nur noch zwei Schritte zu beachten: Es muss derselbe Vorgang für die linke und rechte Seite vorgenommen werden. In diesem Beispiel sind das die Zeilen:

if(links < ptr2) my_qsort(links, ptr2);
if(ptr1 < rechts) my_qsort(ptr1, rechts);

Damit wird der weitere Vorgang rekursiv für beide Seiten ausgeführt. Und zwar so lange, bis die Adresse links kleiner als ptr2 und die Adresse rechts größer als ptr1 ist. Einfach ausgedrückt ist dies der Fall, wenn kein Teilungsprozess mehr möglich ist.

24.3.6 qsort() 

Sollten Sie in der Praxis vorhaben, diesen Algorithmus einzusetzen, können Sie auch den Quicksort-Algorithmus qsort(), der in der Standard-Headerdatei <stdlib.h> implementiert ist, verwenden. Dieser läuft zumeist stabiler und sicherer ab als die Eigenkreation, da Fehler bei der Implementierung seltener sind. Hier nochmals die Syntax zu qsort():

void qsort(void *base, size_t num, size_t size,
           int (*cmp)(void *elem1, void *elem2));

base ist die Adresse des ersten Elements in der Liste oder in einem Array, das es zu sortieren gilt. Die Anzahl der Elemente geben Sie mit num und die Größe der einzelnen Elemente mit size an. cmp ist eine Adresse auf eine Vergleichsfunktion, die Sie selbst implementieren müssen. Schließlich kann qsort() nicht von vornherein wissen, um welche Art von Daten es sich handelt (Strukturen, Arrays, Strings …), die Sie sortieren wollen. So bleibt qsort() immer für den Allgemeingebrauch verfügbar. Hierzu die Funktion qsort() der Standard-Bibliothek im Zeitvergleich mit unserer Eigenkreation:

/* profile_quicksort.c */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 5000000
/* Das Array zum Sortieren */
int test_array[MAX];
void my_qsort(int*, int*);
void init_test_array(void) {
   int i, j;
   for(i = MAX,j=0; i >= 0; i--,j++)
      test_array[j] = i;
}
/* Vergleichsfunktion für qsort() */
int cmp_integer(const void *wert1, const void *wert2) {
   return (*(int*)wert1 – *(int*)wert2);
}
/* Die Funktion erhält einen Zeiger auf das erste
 * und einen zweiten Zeiger auf das letzte Element.
 * Hier werden die Namen links und rechts verwendet
 */
void my_qsort(int *links, int *rechts) {
   int *ptr1 = links;
   int *ptr2 = rechts;
   int w, x;
   /* x bekommt die Anfangsadresse der
    * Mitte von links und rechts
    * Anstatt der Bitverschiebung hätten Sie
    * auch einfach geteilt durch 2 rechnen können.
    */
   x = *(links + (rechts – links >> 1));
   do {
      while(*ptr1 < x) ptr1++;
      while(*ptr2 > x) ptr2--;
      if(ptr1 > ptr2)
         break;
      w = *ptr1;
      *ptr1 = *ptr2;
      *ptr2 = w;
   }while(++ptr1 <= --ptr2);
   if(links < ptr2)  my_qsort(links, ptr2);
   if(ptr1 < rechts) my_qsort(ptr1, rechts);
}
int main(void) {
   clock_t start,ende;
   init_test_array();
   start = clock();
   qsort(test_array, MAX, sizeof(int), cmp_integer);
   ende = clock();
   printf("qsort() der Standard-Library: %.2f\n",
      (float)(ende-start) / (float)CLOCKS_PER_SEC);
   init_test_array();
   start = clock();
   my_qsort(test_array, test_array+MAX);
   ende = clock();
   printf("Selbst geschriebene Quicksort-Funktion %.2f\n",
      (float)(ende-start) / (float)CLOCKS_PER_SEC);
   return EXIT_SUCCESS;
}

24.3.7 Zusammenfassung der Sortieralgorithmen 

Jetzt werden die Sortieralgorithmen ein wenig analysiert. Es soll ein Beispiel erstellt werden, mit dem drei verschiedene Zustände von Daten sortiert werden.

Zuerst sollen Daten sortiert werden, bei denen das größte Element ganz am Anfang ist und absteigend das kleinste Element ganz am Ende.

Anschließend sollen Daten sortiert werden, die bereits in sortierter Form vorliegen. Denn es kann ja immer mal vorkommen, dass Herr Meier die Daten sortiert hat, und Herr Müller weiß wieder mal nichts davon und sortiert diese nochmals.

Im letzten Beispiel werden Daten sortiert, die mit Zufallsdaten belegt werden.

Die Anzahl der Elemente ist in einem solchen Fall natürlich auch entscheidend. Es werden dafür 1000, 10000 und am Schluss 100000 Elemente verwendet, die nach den vorhandenen Zuständen sortiert werden sollen.

Das Programm wurde der Übersicht halber etwas zusammengepresst. Es ist nur die Ausgabe des Programms von Interesse. Leiten Sie die Standardausgabe am besten in eine Textdatei um, indem Sie im Programm noch vor der for-Schleife in der main()- Funktion Folgendes eingeben:

freopen("benchmark.txt", "a+", stdout);

Dies kann jetzt – abhängig vom Rechner – etwas dauern. Hier das kleine Benchmark dazu mit einigen Sortieralgorithmen:

/* sortbenchmark.c */
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#define MAX 100000
/* Ein Array von großen zu kleinen Werten */
int test_array[MAX];
void init_test_array(int elements) {
   int i, j;
   for(i = elements,j=0; i >= 0; i--,j++)
      test_array[j] = i;
}
/* Ein bereits sortiertes Array */
void init_test_array2(int elements) {
   int i;
   for(i = 0; i <= elements; i++)
      test_array[i] = i;
}
/* Ein Array mit (Pseudo)-Zufallszahlen */
void init_test_array3(int elements) {
   int i;
   for(i = 0; i <= elements; i++)
      test_array[i] = rand();
}
/* Vergleichsfunktion für qsort() */
int cmp_integer(const void *wert1, const void *wert2) {
   return (*(int*)wert1 – *(int*)wert2);
}
/* Die Funktion erhält einen Zeiger auf das erste
 * und einen zweiten Zeiger auf das letzte Element.
 * Hier werden die Namen links und rechts verwendet
 */
void my_qsort(int *links, int *rechts) {
   int *ptr1 = links;
   int *ptr2 = rechts;
   int w, x;
   /* x bekommt die Anfangsadresse der
    * Mitte von links und rechts
    * Anstatt der Bitverschiebung hätten Sie
    * auch einfach geteilt durch 2 rechnen können.
    */
   x = *(links + (rechts – links >> 1));
   do {
      while(*ptr1 < x) ptr1++;
      while(*ptr2 > x) ptr2--;
      if(ptr1 > ptr2)
         break;
      w = *ptr1;
      *ptr1 = *ptr2;
      *ptr2 = w;
   } while(++ptr1 <= --ptr2);
   if(links < ptr2)  my_qsort(links, ptr2);
   if(ptr1 < rechts) my_qsort(ptr1, rechts);
}
void shellsort (int *array, int elemente) {
  int i, j, temp, n;
   /* Anfangswert für die Distanz errechnen */
  for ( n = 1; n <= elemente/9; n = 3*n+1);
  for (; n > 0; n /= 3) {
     for (i = n; i <= elemente; i++) {
        temp = array[i];
        /* Größer als temp und nicht elemente
         * sowie >= und nicht > */
        for(j = i;
            j >= n && array[j-n] > temp;
            j -= n) {
           array[j] = array[j-n];
        }
        array[j] = temp;
     }
  }
}
void selection(int *array, int elemente) {
   int i, j, mini, temp;
   for(i = 0; i < elemente; i++) {
      mini=i;
      for(j=i+1; j <= elemente; j++) {
         if(array[j] < array[mini])
            mini=j;
      }
      temp=array[mini];
      array[mini]=array[i];
      array[i]=temp;
   }
}
void insertion(int *array, int elemente) {
   int i, j, temp;
   for(i = 1; i <= elemente; i++) {
      temp=array[i];  /* aktuelles Element zwischenspeichern */
      for(j=i; array[j-1] > temp && j > 0; j--)
         /* So lange der Vorgänger größer ist als das
          * aktuelle Element in temp ... */
         array[j] = array[j-1];
      /* gespeichertes Element an neue Position */
      array[j]=temp;
   }
}
void bubble(int *array, int elemente) {
   int i, temp;
   while(elemente--)
      for(i = 1; i <= elemente; i++)
         if(array[i-1] > array[i]) {
            temp=array[i];
            array[i]=array[i-1];
            array[i-1]=temp;
         }
}
int main(void) {
   int i;
   int elemente=1000;
   float zeit;
   clock_t start, ende;
   /* freopen("log.txt","a+",stdout); */
   for(i=1; i<=3; i++, elemente*=10){
      printf("\n\nSortieren von %d Elementen\n\n",elemente);
      printf("\n%d. Versuch : alle %d Elemente muessen "
             "sortiert werden\n\n",i,elemente);
   /* Selectionsort */
      init_test_array(elemente);  start = clock();
      selection(test_array, elemente-1);  ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Selectionsort: %.2f Sekunden\n",zeit);
   /* Insertionsort */
      init_test_array(elemente);  start = clock();
      insertion(test_array, elemente-1); ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Insertionsort: %.2f Sekunden\n",zeit);
   /* Bubblesort */
      init_test_array(elemente);  start = clock();
      bubble(test_array, elemente);  ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Bubblesort   : %.2f Sekunden\n",zeit);
   /* Shellsort */
      init_test_array(elemente);  start = clock();
      shellsort(test_array, elemente-1);  ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Shellsort    : %.2f Sekunden\n",zeit);
   /* Quicksort */
      if(elemente < 50000){
         init_test_array(elemente);  start = clock();
         my_qsort(test_array, test_array+elemente);
         ende = clock();
         zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
         printf("Quicksort    : %.2f Sekunden\n",zeit);
      }
   /* qsort aus der Standard-Bibliothek <stdlib.h> */
      init_test_array(elemente);  start = clock();
      qsort(test_array, elemente, sizeof(int), cmp_integer);
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("qsort        : %.2f Sekunden\n",zeit);
   /* 2. Versuch, eine bereits sortierte Liste */
      printf("\n%d. Versuch : keins der %d Elemente muss "
             "sortiert werden\n\n",i,elemente);
   /* Selectionsort */
      init_test_array2(elemente);  start = clock();
      selection(test_array, elemente-1);  ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Selectionsort: %.2f Sekunden\n",zeit);
   /* Insertionsort */
      init_test_array2(elemente);  start = clock();
      insertion(test_array, elemente-1);  ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Insertionsort: %.2f Sekunden\n",zeit);
   /* Bubblesort */
      init_test_array2(elemente);  start = clock();
      bubble(test_array, elemente);  ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Bubblesort   : %.2f Sekunden\n",zeit);
   /* Shellsort */
      init_test_array2(elemente);  start = clock();
      shellsort(test_array, elemente-1);  ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Shellsort    : %.2f Sekunden\n",zeit);
   /* Quicksort */
      init_test_array2(elemente);  start = clock();
      my_qsort(test_array, test_array+elemente);  ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Quicksort    : %.2f Sekunden\n",zeit);
   /* qsort aus der Standard-Bibliothek <stdlib.h> */
      init_test_array2(elemente);  start = clock();
      qsort(test_array, elemente, sizeof(int), cmp_integer);
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("qsort        : %.2f Sekunden\n",zeit);
   /* 3. Versuch Zufallsdaten */
      printf("\n%d. Versuch : %d Zufallszahlen muessen"
             "sortiert werden\n\n",i,elemente);
   /* Selectionsort */
      init_test_array3(elemente);  start = clock();
      selection(test_array, elemente-1);  ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Selectionsort: %.2f Sekunden\n",zeit);
   /* Insertionsort */
      init_test_array3(elemente);  start = clock();
      insertion(test_array, elemente-1);  ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Insertionsort: %.2f Sekunden\n",zeit);
   /* Bubblesort */
      init_test_array3(elemente);  start = clock();
      bubble(test_array, elemente);  ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Bubblesort   : %.2f Sekunden\n",zeit);
   /* Shellsort */
      init_test_array3(elemente);  start = clock();
      shellsort(test_array, elemente-1);  ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Shellsort    : %.2f Sekunden\n",zeit);
   /* Quicksort */
      init_test_array3(elemente);  start = clock();
      my_qsort(test_array,test_array+elemente);   ende = clock();
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("Quicksort    : %.2f Sekunden\n",zeit);
   /* qsort aus der Standard-Bibliothek <stdlib.h> */
      init_test_array3(elemente);  start = clock();
      qsort(test_array, elemente, sizeof(int), cmp_integer);
      zeit = (float)(ende-start) / (float)CLOCKS_PER_SEC;
      printf("qsort        : %.2f Sekunden\n",zeit);
   }/* Ende for */
   return EXIT_SUCCESS;
}

In der folgenden Tabelle finden Sie eine Analyse der einzelnen Sortierfunktionen. Bei einigen Algorithmen wurde die Anzahl der Elemente nochmals erhöht, da diese bei den Anforderungen eine kaum nennenswerte Zeit benötigen.

Mithilfe dieser Analyse können Sie sich nun ein etwas detaillierteres Bild von der Effizienz der einzelnen Algorithmen machen. Natürlich sollten Sie diese Laufzeitmessung nicht allzu genau nehmen. Für eine exaktere und genauere Messung sollten Sie auf jeden Fall einen Profiler einsetzen. Denn das Programm zur Laufzeitmessung ist während der Ausführung sicherlich nicht das einzige Programm, welches gerade auf Ihrem System läuft.

Die Frage nach dem besten Algorithmus lässt sich allerdings auch mit solch einer Analyse nicht exakt klären. Diese ist auch sehr abhängig von der Verteilung und Art der Daten, die es zu sortieren gilt. Außerdem ist es auch möglich, die einzelnen Algorithmen weiter zu optimieren. Beim Thema Algorithmen kommen Sie nicht darum herum, weitere Literatur zu Rate zu ziehen.