#####____________________Datentypen float und double___________________

Jetzt lernen wir die Fließkommavariablen (Floatingpoint) kennen. Damit wird es uns nun endlich möglich sein genauere Berechnungen nach dem Komma anzustellen. Hier wieder eine kleine Übersicht...

Name Größe Wertebereich Formatzeichen

float 4 Bytes 3.4*10^-38....3.4*10³⁸ %f

double 8 Bytes 1.7*10^-308....1.7*10³⁰⁸ %lf

long double 10 Bytes 3.4*10^-4932....3.4*10⁴⁹³² %lf

Alle Zahlen oben haben mindestens einen Wertebereich von 10³⁸ bis 10^-38. Das heißt 10*10*10*10*....(34 weitere *10). Angewendet werden diese Variablentypen genauso wie 'int' und alle andere Typen.

Es muss auch erwähnt werden das Gleitkommazahlen eigentlich Gleitpunktzahlen heißt, da die Programmiersprache C in Amerika entwickelt wurde. Und dort wird anstatt eines Kommas zwischen den Zahlen ein Punkt verwendet....

float a=1,5; //FALSCH float b=1.5; //RICHTIG

Das Komma verwenden die Amerikaner wieder genauso wie wir die Punkte bei Größeren Zahlen verwenden. Beispiel 1 Millionen schreiben wir oft so....

1.000.000

...die Amerikaner wiederum schreiben 1 Millionen so....

1,000,000

...mit Kommas. Dies nur zur Information nebenbei.

Am besten sehen wir uns dazu ein Beispiel an. Wir wollen das Volumen einer Kugel berechnen...

/*Download:float1.c*/
#include <stdio.h>

int main()
{
float Volum,durchm,Pi;
Pi=3.14; /*für unsere Zwecke reicht die Genauigkeit*/
printf("Durchmesser der Kugel : ");

scanf("%f",&durchm);
Volum=0.75*(durchm*durchm*durchm/8);

printf("Volumen der Kugel = %f\n",Volum);
return 0;
}

Zur Erklärung der Berechnung: Das Volumen wird berechnet aus...

Pi *Durchmesser³ / 6

Für Pi hätten wir die Stellen nach dem Komma auch genauer eingeben können.

Wenn sie bei Durchmesser der Kugel eine Kommawert eingeben wollen müssen sie einen Punkt anstatt einen Komma verwenden. Also '23,33' ist falsch. Richtig ist '23.33'.

Nun noch etwas wichtiges zu Fließkommazahlen. Wenn man zwei Verschieden Variablen ,z.B 'int' und 'float' miteinander durch Operatoren verknüpft bekommen sie das Ergebnis des genaueren Typen dieser beiden Variablen. Dazu ein Programmbeispiel...

/*Download:float2.c*/
#include <stdio.h>

int main()
{
float f;
int i;

f=5.0;
i=2;

printf("%f\n",f/i); /*Ergebnis = 2.500000*/
return 0;
}

Nun kennen sie 2 verschiedene Datentypen für Gleitpunktzahlen. Welche von diesen beiden eignet sich denn nun besser dafür? Um das besser zu verstehen wollen wir doch Gleitkommazahlen etwas genauer betrachten.

(Tausend Dank an Philipp Gühring von Futureware 2001 der mir diesen Text zur Verfügung gestellt hat)

Gleitkommadarstellung

Bei dieser Darstellung wird die Position des Dezimalpunktes einer Zahl zusätzlich dynamisch geregelt. Unangenehmerweise ist es möglich, ein und dieselbe Zahl auf verschiedenste Arten darzustellen. Zum Beispiel...

0,123 = 123 * 10^-3 = 1230 * 10^-4 = 12300 * 10^-5

Darum wurde für die Gleitkommadarstellung die normierte Form entwickelt: Die Mantisse ist eine Zahl, deren Vorkommateil 1 ist. Einzigster Problemfall: Die Zahl 0. Die restliche Information der Zahl ist im Nachkommateil der Mantisse und im Exponenten der Zahl. Also...

Zahl = 1,Mantisse*Basis^Exponent

Normiert man z.B. die binäre Zahl...

+11001,1011

...sieht das Ergebnis folgendermaßen aus...

+1,10011011 * 10¹⁰⁰

Da die Ziffer vor dem Komma also fast immer 1 ist (Ausnahme: 0), kann man auf deren Abspeicherung verzichten und gewinnt so ein zusätzliches Mantissenbit, wodurch die Genauigkeit erhöht werden kann. Diese Genauigkeit wird allerdings mit der Sonderbehandlung von 0 erkauft. Es muß also nur das Vorzeichen (1 Bit), die sogenannte Mantisse und der Exponent abgespeichert werden.

Charakteristik

In der Praxis treten positive Exponenten häufiger auf als negative. Man vergrößert daher den Bereich für positive Exponenten auf Kosten der negativen Exponenten. Das geschieht dadurch, daß zum Wert des Exponenten ein konstanter Betrag k addiert wird. Diese Konstante k wird als Charakteristik bezeichnet. Bsp.:

k=4; darzustellender Wert: 173d r +173 = 10101101 binär = 0,101011010 * 2⁸ normalisiert. Darstellung des Exponenten 8-4 = 4 = 100 binär.

An diesem Beispiel kann man die Vergrößerung in Richtung der positiven Zahlen deutlich sehen: Die Zahl 173 könnte ohne Charakteristik in diesem Format gar nicht dargestellt werden, da der Exponent 8 ist (Binär: 1000) und 3 Bits im Exponenten für die Darstellung von 8 nicht reichen würden.

Genauigkeit der Nachkommastellen

float ist eine 32Bit Zahl und seine einfache Genauigkeit beträgt 24Bit. Die 32Bit teilen sich folgendermaßen auf...

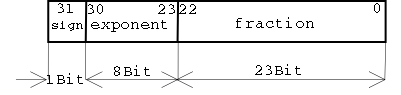
sign : In Bit 31 wird das Vorzeichen der Zahl gespeichert. Ist diese 0, dann ist die Zahl positiv. Und bei 1 ist sie Negativ da das Vorzeichenbit gesetzt ist.
exponente : Hier wird die exponente der Zahl gespeichert.
fraction : Hier wird der Bruchteil der Mantisse gespeichert.

double ist eine 64Bit Zahl und seine doppelte Genauigkeit beträgt 53Bit und ist folgendermaßen aufgeteilt.....

double

sign : In Bit 63 wird das Vorzeichen der Zahl gespeichert. Ist diese 0, dann ist die Zahl positiv. Und bei 1 ist sie Negativ da das Vorzeichenbit gesetzt ist.
exponente : Hier wird die exponente der Zahl gespeichert.
fraction : Hier wird der Bruchteil der Mantisse gespeichert.

Wie werden diese Zahlen nun in der Programmiersprache C abgespeichert?

/*Download:float3.c*/

#include <stdio.h>

int main
{

  float a = + 5.0; /*0x40A00000*/
  float c = -25.5; /*0xC1CC0000*/
  return 0;
}

In folgenden Schritten werden diese Zahlen abgespeichert...

Schritt 1: a = + 5,0d Schritt 2: a = 101b * 10b^0 Schrift 3: a = 1,01b * 10b^(10 + 01111111=10000001) Schrift 4: a = \,01b * 10b^(10 + 01111111=10000001) gespeichert wird: 0 10000001 01000000000000000000000 V Exponent Mantisse Speicherstelle von a: 0x40A00000 Schritt 1: c = - 25,5d Schritt 2: c = - 11001,lb * 10b^0 Schritt 3: c = - l,10011b * 10b^(110 + 01111111 = 10000011) Schritt 4: c = - \,10011b * 10b^(110 + 01111111 = 10000011) gespeichert wird: 1 10000011 100110000000000000000000 V Exponent Mantisse Speicherstelle von c: 0xC1CC0000

Eine Fließkommazahl mit achtstelliger Genauigkeit wie zum Beispiel bei float kann nicht immer achte Dezimalstellen unterscheiden. Wenn zum Beispiel die Zahl vor dem Komma wie z.B. 12345,12345 bereits 5 Stellen besitzt, so kann sie nach dem Komma nur noch 3 Stellen unterscheiden. Somit wäre die Gleitpunktzahlen .....

12345,12345 und 12345,123999

...für den Computer nicht zu Unterscheiden. Mit achtstelliger Genauigkeit sind die signifikanten Stellen von links nach rechts gemeint.

Somit ist die float - Zahl eigentlich ungeeignet für kaufmänische Berechnungen. Sie können ja mal folgendes Beispiel testen...

/*Download:euro_dm.c*/
#include <stdio.h>

int main()
{
float x=1.9643;
float dm=100000.12;
float end_float;

double y=1.9643;
double DM=100000.12;
double end_double;

printf("%f Euro mit float\n",end_float=dm*x);
printf("%lf Euro mit double\n",end_double=DM*y);

return 0;
}

Bei mir sieht die Ausgabe dann wie folgt aus...

196430.233834 Euro mit float 196430.235716 Euro mit double

float ist nun mal nach 8 Dezimalstellen am Ende. Mit double haben sie dagegen die Möglichkeit eine 14 stellige genaue Zahl zu erhalten.

Was kann man nun aber tun wenn einem diese Genauigkeit nicht ausreicht?
In diesem Falls müssen sie sich nach Festkomma-Algorithmen umsehen. Denn Festkommadarstellungen wie die BCD-Arithmetik gibt es in C nicht.

Allgemeine Numerische Probleme

Ungenauigkeiten durch die binäre Darstellung
Reelle Zahlen können im Gleitkommaformat nicht immer exakt dargestellt werden. Dadurch kann es bei der Berechnung von arithmetischen Ausdrücken zu Ungenauigkeiten kommen. Beispiel: 0,1d=0,00011001100110011...b Beispiel 0,11; 0,2; 0,4, usw. können nicht genau dargestellt werden.

Daher: Zahlen im Gleitkommaformat (float,double,...) nie auf Gleichheit prüfen! Statt dessen Prüfung auf > oder < oder E-Bereich. Folgendes Programm wird in eine Endlosschleife laufen, da die Zahl 0.1 nie exakt dargestellt werden kann....

/*Download:float4.c*/
#include <stdio.h>

int main()
{
float i=0.0;
for (i=0.0; i != 1.0; i += 0.1)
printf("%f",i);

return(0);
}

Sicherere ist es wenn sie diese Beispiel im E-Bereich prüfen...

/*Download:float5.c*/
#include <stdio.h>

int main()
{
float i=0.0;
for (i=0.0; i<0.9999 || i>1.0001; i += 0.1)
printf("%f",i);

return(0);
}

Fehler durch Zwischenergebnisse

Bei der Berechnung arithmetischer Ausdrücke kommt es durch Rundungsfehler und Überlauffehler bei Zwischenergebnissen zu Ungenauigkeiten. Beispiel: 5-stellige ganze Zahlen A = 00900 B = 10000

A * B / 100 = 00000 A *(B / 100) = 90000 (A * B) / 100 = 00000

Es muss also auf die Reihenfolge der Auswertung geachtet werden. Bei der technischen Arithmetik gilt NICHT

das Assoziativgesetz
das Distributivgesetz

Sondern es gilt......

a + (b + c) < a * (b + c) <

Beispiel (8 Bit Format): a = 11,0000 b = 0,0000 11 c = 0,0000 1 a = 11,0000 + (b+c)= 0,0001 -- ================= a+ (b+c)= 11,0001 -- (a+b) = 11,0000 -- +C = 0,0000 -- ==================== (a+b)+c = 11,0000 --

Wie man sieht, sind beide Ergebnisse unterschiedlich.

Aufgabe : Schreiben sie ein Programm das eine Kreisfläche berechnet. Die Formel lautet...

Kreisfläche=Durchmesser²*Pi/4

Hier geht's zur Lösung!